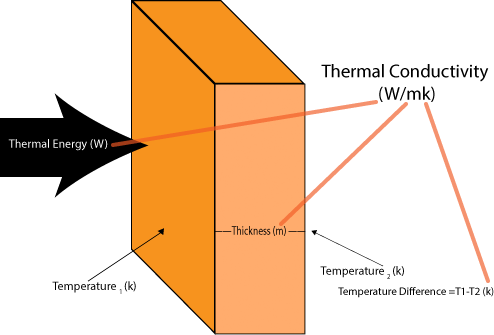
Thermal conductivity is the number of watts (W) conducted per meter (m) of thickness per temperature (kelvin (k)) difference between one side and the other of the material at that thickness. It is reported as W/mk. The inverse of thermal conductivity is thermal resistance.
It is important to know the effective thermal conductivity when designing heat pipes. The thermal conductivity will vary with the heat pipe length, unlike solid metals. For example, the thermal conductivity of copper is 390 W/m-k, but for heat pipes, it can range from 1,500 W/mk to 50,000W /mk.
The thermal conductivity of a solid metal stays constant because the heat transfers through molecules that are the same and therefore offer the same thermal resistance. For a copper heat pipe, there are multiple stages of heat transfer and thermal resistance. The heat passes through the metal envelope and vaporizes the liquid. The resistance of the vaporized liquid traveling down the heat pipe is minimal, so the thermal conductivity is higher. The longer the heat pipe, the higher the thermal conductivity.
It should be noted that the effective length of a heat pipe is not its actual length; it is the heat pipe distance from the midpoint of the evaporator to the midpoint of the condenser.
The diameter of the heat pipe matters, too. Small diameter heat pipes have a higher effective thermal conductivity than larger diameter heat pipes. The effective thermal conductivity goes down by the ratio of the cross-sectional area.
Thermal conductivity can be calculated as follows:
Keff = Q Leff /(A ΔT)
where:
Keff = Effective thermal conductivity (W/mK)
Q = Power transported (W)
Leff = Effective length = (Levaporator + Lcondenser)/2 + Ladiabatic (m)
A = Cross-sectional area [m2]
ΔT = Temperature difference between evaporator and condenser sections (°k)
Contact KTK
Have questions about heat pipes or need assistance with thermal management, contact us.
